이제 전처리 단계로 넘어 갑시다.
EDA와 데이터 프레임을 다양한 형태로 통합하는 이전 프로세스 덕분에 전처리가 상대적으로 쉬워졌습니다.
우리가 다룰 df_norm 데이터 유형부터 시작하겠습니다.

여기서 입력 결과에 따라 Pres_DEM, Pres_REP, Gov_DEM 및 Gov_REP를 제외하고 값이 NaN인 데이터를 삭제하겠습니다.
df_norm.dropna(inplace = True)
X = df_norm.drop(('Pres_DEM', 'Pres_REP', 'Gov_DEM', 'Gov_REP'), axis = 1)
y = df_norm('Pres_DEM')위의 칼럼에서 볼 수 있듯이 해당 변수는 모두 수치 데이터이므로
표준화는 추가적인 노력 없이 수행될 수 있습니다.
from sklearn.preprocessing import StandardScaler
# StandardScaler를 이용해 수치형 데이터를 표준화하기
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
X = pd.DataFrame(data=X_scaled, index= X.index, columns = X.columns)모든 열에 대해 X가 잘 표준화되어 있음을 알 수 있습니다.
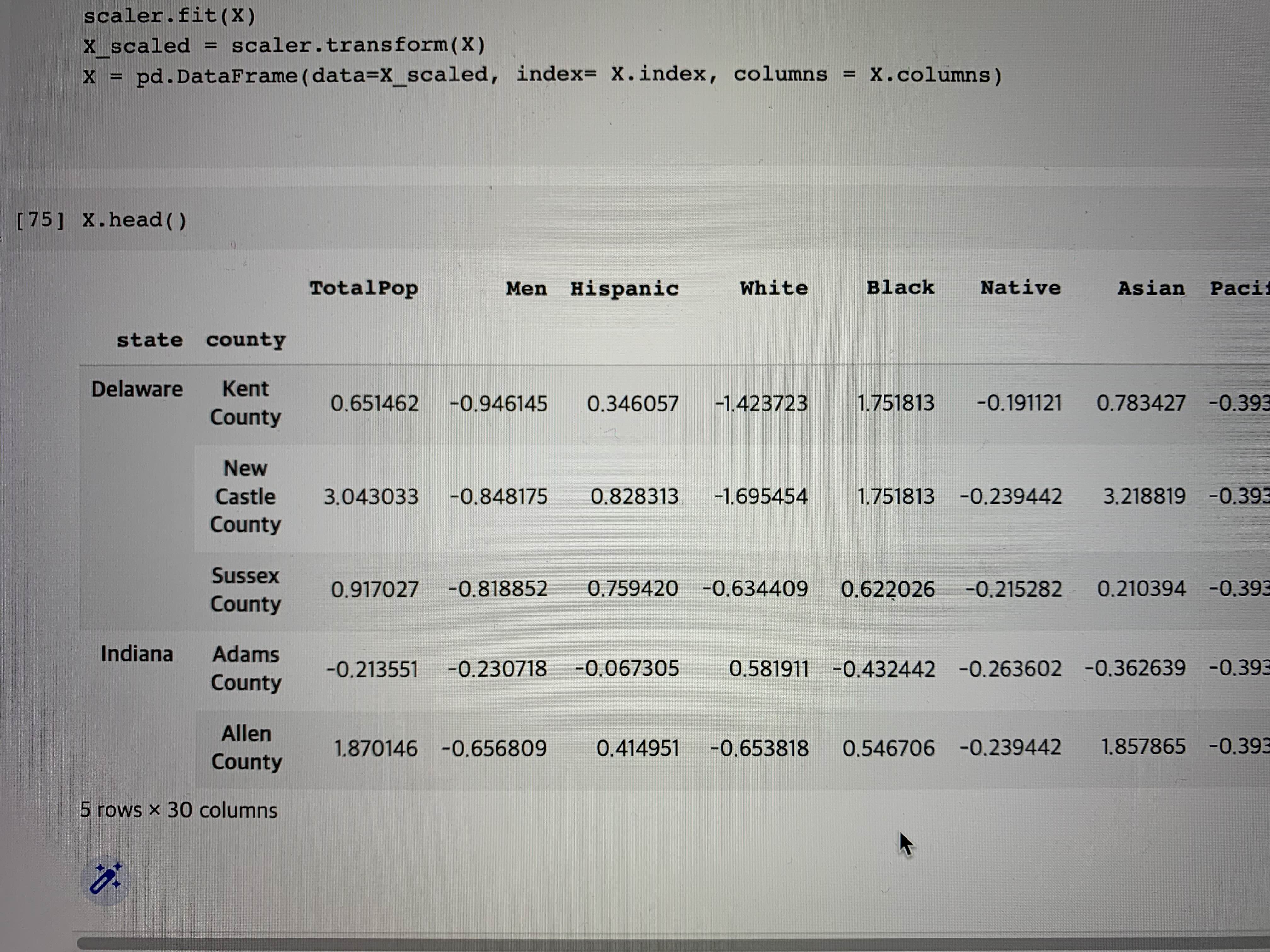
이후 train과 test data를 분리하는 과정도 이전과 동일하다.
from sklearn.model_selection import train_test_split
# train_test_split() 함수로 학습 데이터와 테스트 데이터 분리하기
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 1)이전 강의에서는 바로 모델링 프로세스에 들어갔습니다.
이번 강의에서는 PCA에 의한 데이터 전처리를 추가적으로 진행하는 과정을 담았다.
먼저 코드 및 결과와 함께 PCA를 자세히 요약해 보겠습니다.
from sklearn.decomposition import PCA
# PCA를 이용해 Dimensionality Reduction 수행하기
pca = PCA()
pca.fit(X_train)
plt.plot(range(1, len(pca.explained_variance_) + 1), pca.explained_variance_)
plt.grid()
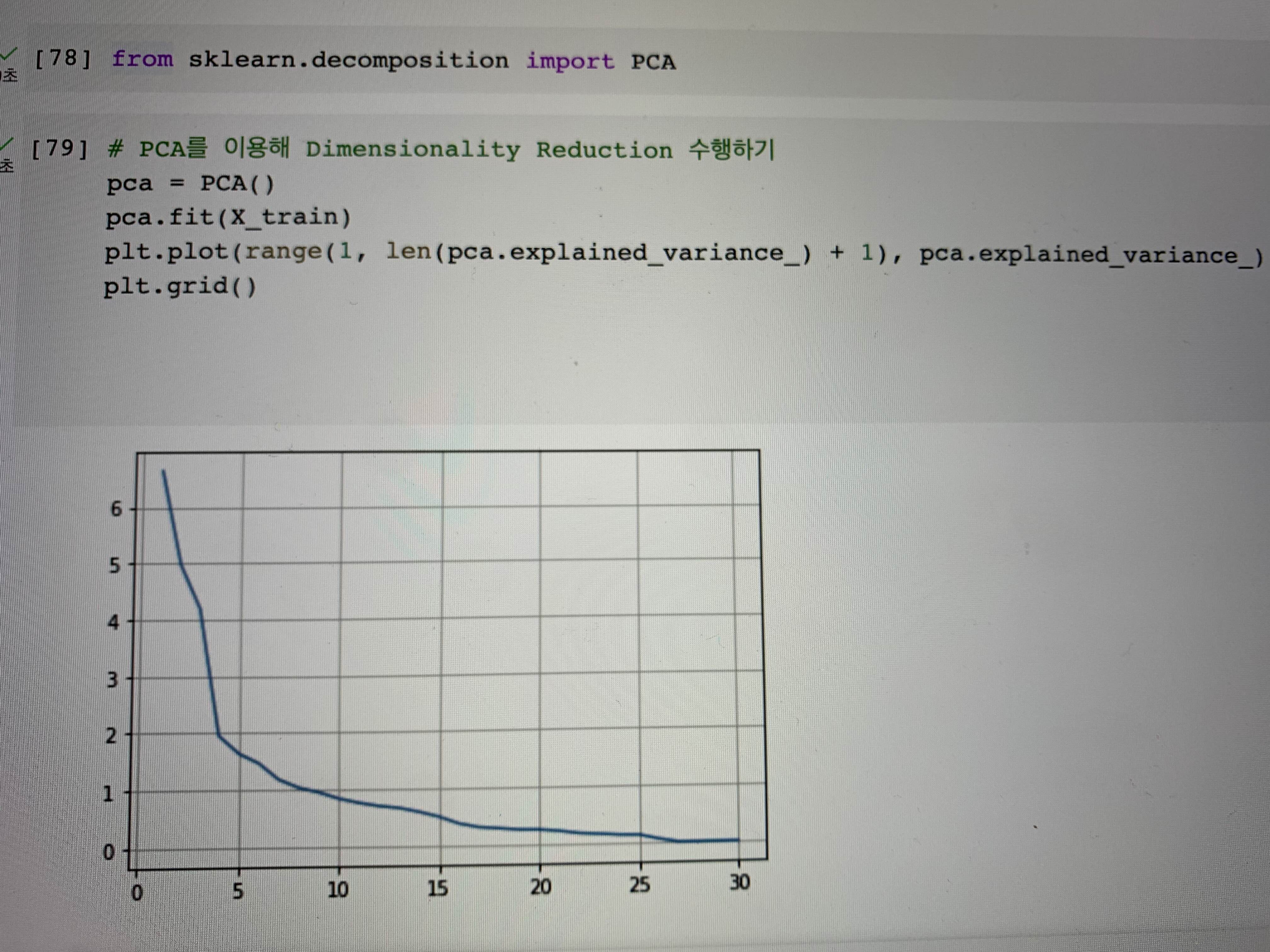
PCA(Principal Component Analysis)는 고차원 데이터를 저차원 데이터로 줄이는 기술 중 하나입니다.
세부 파라미터 설정은 다음과 같습니다.
- n_components: 줄일 차원 수. 기본값은 없음이며 이 경우 모든 주요 구성 요소가 유지됩니다.
- 흰색으로 설정하는 경우: True, 고유 벡터는 서로 직교하고 분산은 1로 설정되어 특징 벡터를 흰색으로 만듭니다. 기본값은 거짓입니다.
- svd_solver: SVD 알고리즘을 지정합니다. 자동, 전체, arpack, 무작위 중에서 선택할 수 있으며 기본값은 자동입니다.
- random_state: 난수 생성을 위한 시드, 기본값은 없음
또한 PCA를 적용한 결과는 fit_transform 메소드를 이용하여 계산할 수 있는데, 이때 분석할 데이터를 입력값으로 사용하면 PCA로 변환된 데이터가 반환된다.
# 코드 예시
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
reduced_data = pca.fit_transform(data)위의 코드에서 n_components를 2로 설정하여 데이터를 2D로 축소하고, 분석할 데이터를 fit_transform 메소드를 사용하여 변환한 결과를 Reduced_data에 저장합니다.
또한 PCA로 얻은 주성분은 components_attribute로 확인할 수 있다. 전체 분산에 대한 각 주성분의 비율은 “explained_variance_ratio_” 속성을 통해 확인할 수 있습니다.
마지막으로 PCA 결과를 시각화하기 위해 matplotlib 라이브러리를 사용하여 산점도를 그릴 수 있습니다.
## 예시
# 주성분 비율로 확인하기
components = pca.components_
explained_variance_ratio = pca.explained_variance_ratio_
# 산점도로 표현하기
import matplotlib.pyplot as plt
plt.scatter(reduced_data(:, 0), reduced_data(:, 1))
plt.show()PCA는 소수의 주성분으로 구성된 새로운 데이터를 개념화하기 위해 데이터의 구조를 최대한 유지하면서 데이터의 차원을 줄이는 데 사용할 수 있습니다. 이를 통해 고차원 데이터를 시각화하거나 분석에 사용할 수 있습니다.
위의 데이터를 보면 차트의 추세가 급격하게 꺾이는 지점을 찾아 n_components를 결정할 수 있습니다.
먼저 10으로 설정한 다음 모델링을 계속하겠습니다.
본 포스팅은 패스트캠퍼스 환불 챌린지 참여를 위해 작성되었습니다.